前言
在博客建立之初,我第一次尝试访问博客
意外地出现了以下情况:
在稍微时搜索后,初次认识到“密码学”这个概念
注:以下内容系个人理解,仅供参考。部分内容可能存在误解,还请多加指正。
恺撒密码
初为程序员,我想大家几乎都接触过这个东西
作为最早的对称加密算法,兼具加解密一体的特性
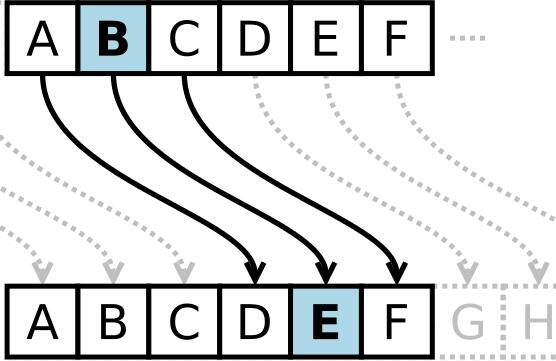
恺撒密码原理
简单来说,就是将字母表偏移,得到新的字母表
然后将原文按照偏移量将每个字符替换为新的字符,得到密文
当接收方获得密文后,再根据协商好的偏移量,反向解出原文
当然,这种方法的安全性非常低,很容易根据字符统计何语法规律推算出偏移量
从而暴力破解出原文
维吉尼亚密码
后来,维吉尼亚密码横空出世,采用了多表替换形式组合成了一套更为复杂的凯撒密码
 维吉尼亚密码(图片自维基百科)
维吉尼亚密码(图片自维基百科)
维吉尼亚密码原理
利用明文与秘钥组合的方式加密
比如,原文:RCHIZONE 秘钥:DEAGIF
则以RCHIZONE为列(行),DEAGIF为行(列)写出密文
这里显然秘钥对应原文字符量不足,则可以将秘钥扩展两倍:DEAGIFDEAGIF
密文:UGHOHTQI
解密方法则以秘钥为行(列),找到这一行中的密文所对应的列(行)
 此处为对应密文前四位解密
此处为对应密文前四位解密
代码如下
加密代码: Vigenere.java
解密代码: DeVigenere.java
此代码为默认使用字母表顺序,更复杂的方法则可以通过自定义密码表或延长秘钥长度来实现,此处则不做过多展开
密码机
后来,二战时期恩尼格玛机将这类型密码应用到极致,将密码组合拓展到数以亿亿计,让得人工破解成为妄想
在经过图灵等一众科学家的努力,终于破解了恩尼格玛机,提前结束了战争,并促进了计算机的发展
 恩尼格玛机
恩尼格玛机
隐写术
这个对于普通人最容易理解,也容易实现
比如藏头诗、隐形墨水、错别字、荧光、摩斯电码、密文加粗、铅笔描纹法和音调转换等等。
 铅笔描纹法
铅笔描纹法
随着数字媒体时代的到来,人们对于网络传递信息的需求日益增长
图像、音频、视频、文本和网页等,都可以成为传递密文的载体
Cicada 3301
 蝉3301
蝉3301
2012年1月4日,4chan用户发布了一张图片
图片中声明要求在该图片中找到隐藏的信息
通过文本编辑器打开图片,可以看到文件的最底部写着这样一段话
TIBERIVS CLAVDIVS CAESAR says
"lxxt>33m2mqkyv2gsq3q=w]O2ntk"
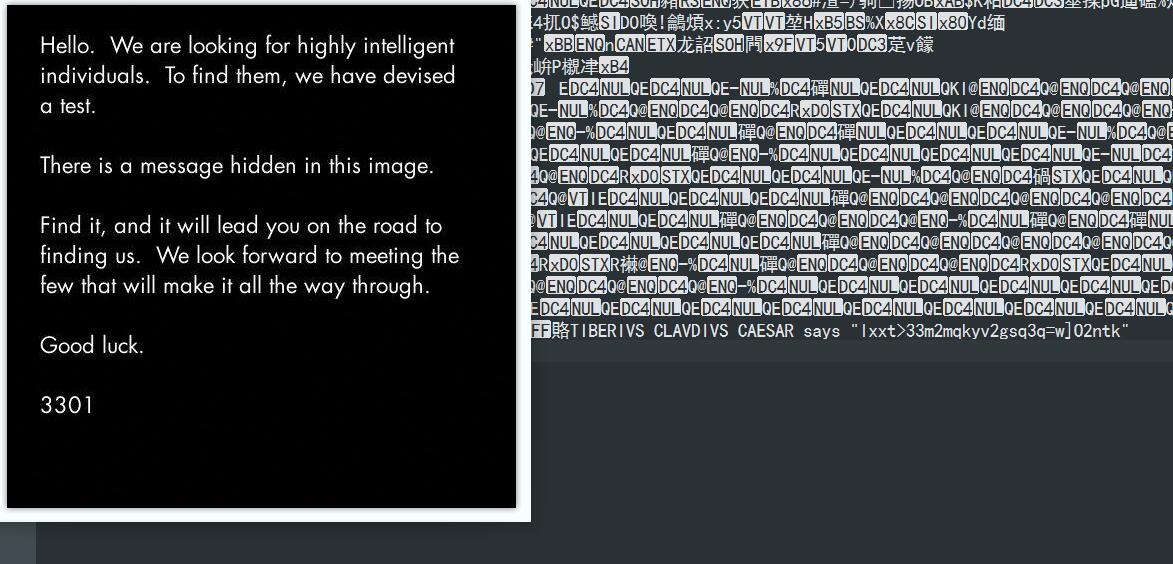
这段话译为: 提贝里乌斯·克劳狄乌斯·凯撒说:lxxt>33m2mqkyv2gsq3q=w]O2ntk
显然这是上文中提到的凯撒密码
在经过一系列破译后,最终被引导到一个链接,这就是最简单的编辑文件内容的隐写术
不过在链接的引导下,随之而来的谜题则越来越难
这其中,有要求将图片中3个数字相乘,其中包括3301,得到结果加上.com
在解密后发现是将图片的 宽度*高度*3301 得到的数字变成一段网址: www.845145127.com
所以在不知情的情况下,你永远无法想象一张图片能藏多少信息。
隐写术的目的是不被发现存在隐藏的信息,从而瞒天过海
LSB
最低有效位(least significant bit, LSB)
在一开始提到的几种常见隐写方法实际上大部分都是LSB技术
在数字媒体下,LSB体现更多的是更改图像的像素颜色
在图像中,每张图片以像素为单位表示
每个像素为由RGB表示
如果将要隐藏的信息转换为二进制,并通过像素颜色参数的微小变化来表示,比如通过±1的方式将奇数表示为1,偶数表示为0,那么就可以利用肉眼难以察觉的方式来隐藏信息。
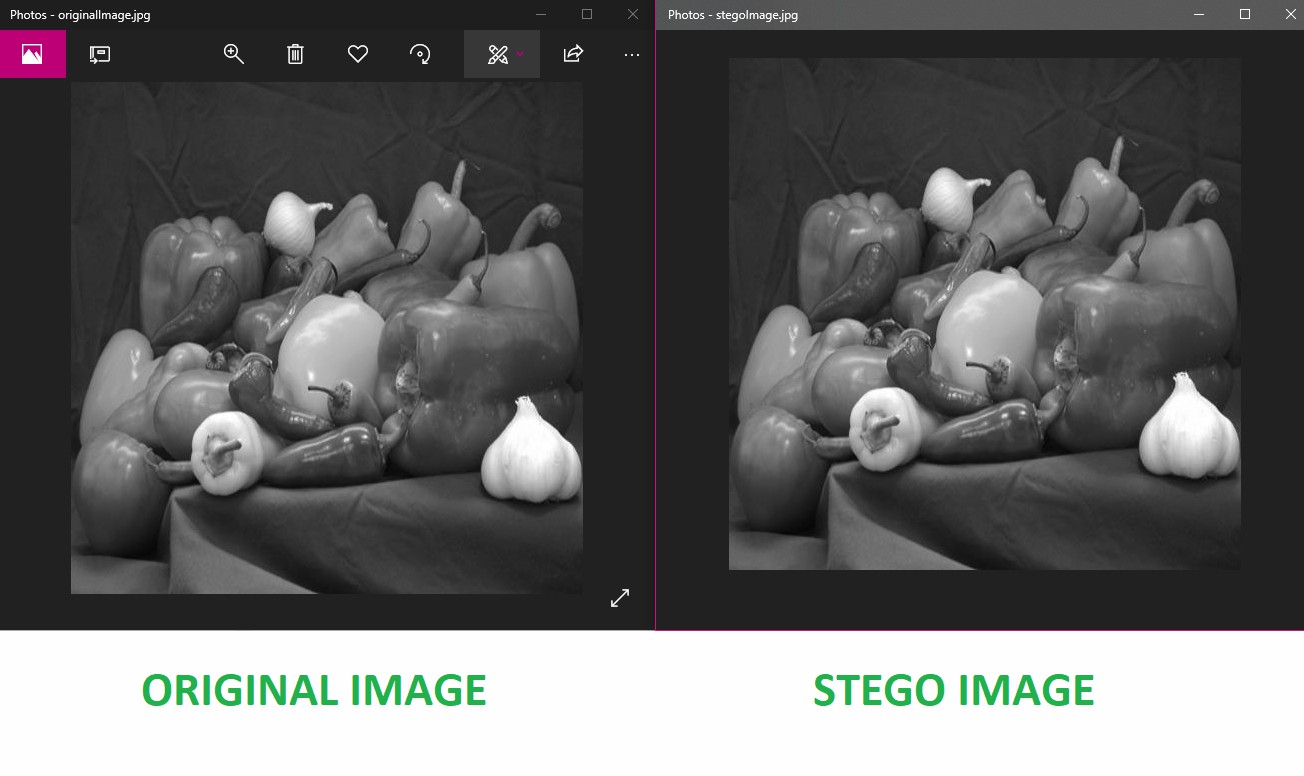
但不过既然你可以通过计算机方式隐写,我也可以利用计算机来统计每个像素,从而识别出这张图片是否被隐写。
结果就暴露了这张图片其一开始的目的
这类方法更具娱乐化的体现方式就是幻影坦克
 幻影坦克
幻影坦克
湖城静丸
2009年,Reddit上出现了一个奇怪的用户: ReligionOfPeace
这个家伙名下有一个网站: www.lakecityquietpills.com
目前这个网站已经失效,在那之前这个网站是一个不受监管的私人图片托管网站
直到某天,ReligionOfPeace在一个随机板块声称一场暗杀,并再次提及到了lakecityquietpills,这个网站被重新审视
在一系列调查下,大家发现个网站的主页是lakecityquietpills.com/photo/multihost/index.php
而不是lakecityquietpills.com
如果访问lakecityquietpills.com 则只会出现空白页
随后,当调查人员查看了页面源代码后,这个这个网站黑暗的一面渐渐浮上水面

显然,网站在别有用意地暗中招聘刺客
2010年1月19日,哈马斯军事组织的一名领导人哈茂德·马巴胡赫在迪拜一家酒店遇害
这与网站上举办“哀悼派对”时间点出奇的一致,使人无不联想到这是一场精心伪装的暗杀行动
但是,就像互联网上的诸多谜题一样,一切都只是猜测而已,并没有实质性的证据
直至今日,仍然没人知道这个网站的目的是什么
深网、暗网
 tor洋葱路由
tor洋葱路由
现在,大家或多或少都接触到过一些关于深网和暗网的相关内容
简单来讲就是无法被搜索引擎(百度,Google等)直接搜索发现的网站
关于这些,这里将不会详细探讨
希尔密码
1929年,美国科学家莱斯特·希尔(Lester S. Hill)通过线性变换提出了希尔加密算法
 密码表
密码表
对于明文信息,可以通过以上密码表将每个字符转换为数字
当然,这种密码表也可以自定义撰写成其他语言的版本
希尔密码原理
在明文转换为数字后,可以将这n个数字拆成每x个为一组的(n/x)个矩阵
然后根据逆矩阵的逆运算性质,明文x、密文y、秘钥A 存在着这样一个关系
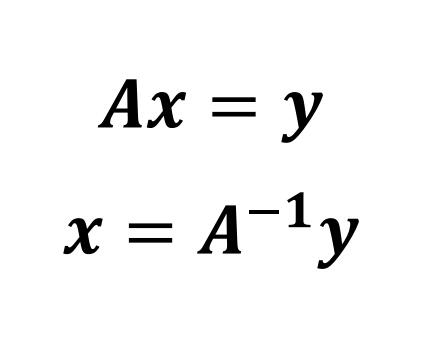 逆矩阵
逆矩阵
加密
- 将RCHIZONE按照三个字符一组拆分(如果不够则用空格补充): RCH, IZO, NE
- 根据上文密码表将明文转换成数字: x1=[18, 3, 8], x2=[9, 26, 15], x3=[14, 5, 0]
- 然后声明一个3×3的可逆矩阵当做秘钥:
- 按照矩阵乘法运算得到密文
- 最终算出y1, y2, y3:
- 经过模运算mod(26)|(求余运算:y%26)得到可以对应密码表的密文: UUXIGESG
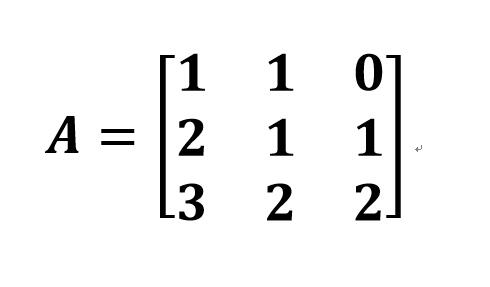
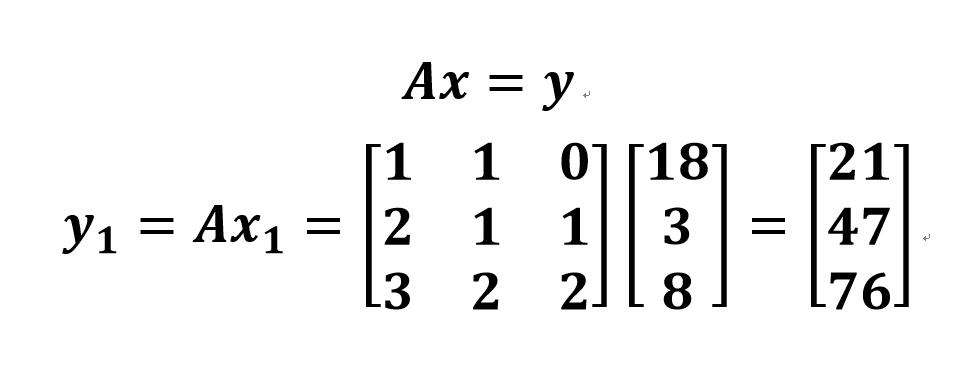
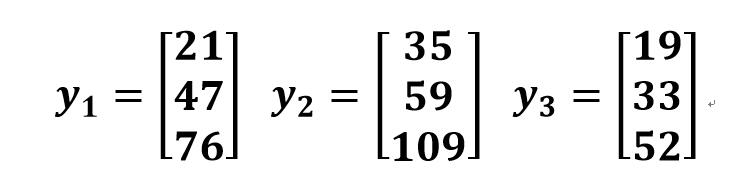
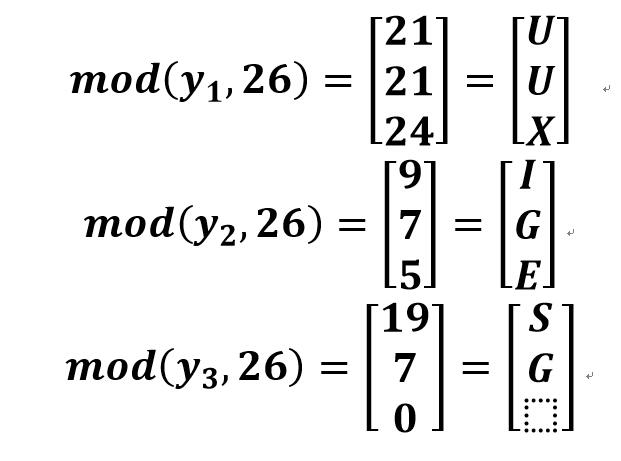
解密
- 同样将密文 UUXIGESG 转换为数字: [21, 21, 24], [9, 7, 5], [19, 7, 0]
- 同时将秘钥 A 进行逆运算得到 A-1:
- 按照矩阵乘法运算解出明文:
- 最终算出x1, x2, x3:
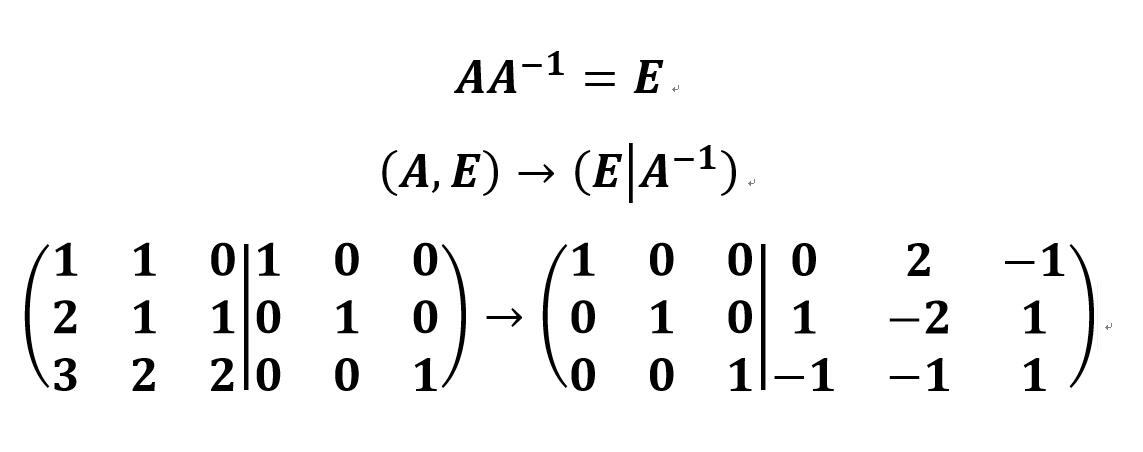 初等变换法
初等变换法
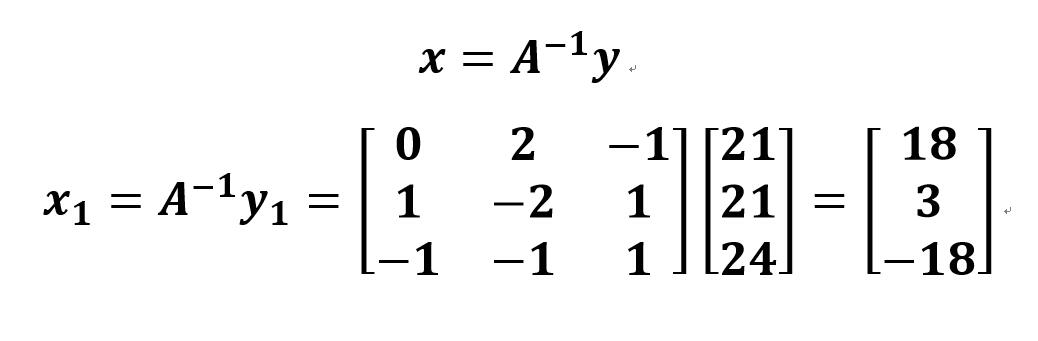
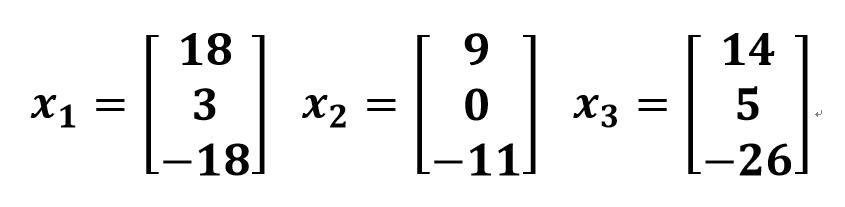
经过模运算mod(26)|(求余运算:y%26)得到可以对应密码表的明文: RCHIZONE

代码如下
加密代码: HillEncrypt.java
解密代码: HillDecrypt.java
不难看出,希尔密码与维吉尼亚密码原理不同,但是方法是相同的
二者都是采用对称加密的方法来处理信息,即加密方与解密方均使用相同秘钥
虽然严格来说希尔密码是将秘钥进行逆运算来进一步解密,但这仍然算是一种对称加密
那么有没有一种方法无法从 加密秘钥 推导出 解密秘钥 呢?
RSA
1977年,麻省理工学院三个人提出了一种非对称加密算法: RSA
在这之前需要理解几个数学概念
- *互质*
- 当两个数字互质时,它们的最大公约数是1
- 比如: 8 和 10 都可以被2整除,那么 8 与 10 不是互质关系
- 7 和 3 的最大公约数是 1,因此 7 与 3 互质
- *欧拉函数*
- 指一个正整数N,比N小且与N互质的个数
- 比如,N=10,那么小于N且与N互质的有四个: 1、3、7、9
- 那么 10 的欧拉函数就是: 4
- 公式记作:
- 这其中,有几种特殊情况:
- 第一种情况: 如果N是质数,那么φ(N)=N-1
- 第二种情况: 如果N=p*q,p与q都是质数且p≠q则有以下等式:
- *欧拉定理*
- 利用欧拉函数,可以得出欧拉定理:
- 如果a与N互质,则aφ(N)%N≡1
- 同理aφ(N)的任意次方,akφ(N)%N≡1 同样成立
- 即 a的φ(N)次方除以N,其余数永远都是 1
- 根据欧拉函数第一种情况,如果N是质数那么aN-1%N≡1
- *模反元素*
- 如果正整数a和n互质,那么可以找到至少一个b,使得a*b%n≡1
- 即存在b,使ab除以n,其余数等于 1
- 比如,4与9互质,那么需要找到一个数b使得等式 4*b%9=1 成立
显然,b不只有一个 [..., 7, 16, 25, 34, 43, 52, ...]都能使等式成立 - 那么b就是a对n的模反元素
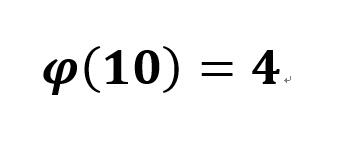
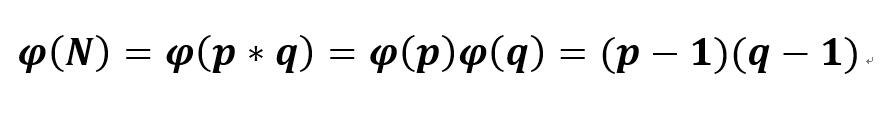
其他情况暂且不考虑
RSA原理
原文: m | 密文: c
公钥 (N, e) | 私钥 (N, d)
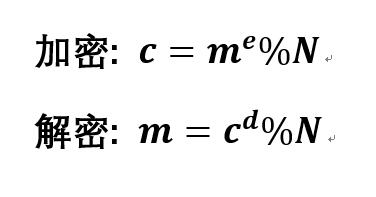
关于N, e, d的选取,以及加解密公式的证明则根据以上的数学概念展开讨论
公式证明
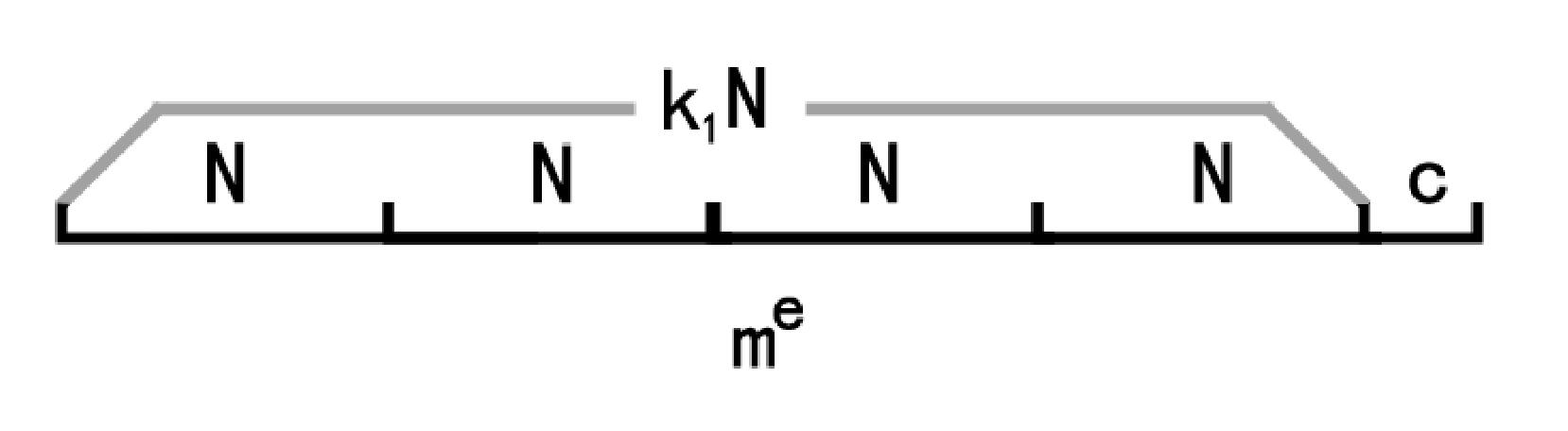
- 根据加密公式,可以得出: me=k1N+c
- c=me-k1N
- 将c代入解密公式 m=cd%N 中
- (me-k1N)d%N=m
- 如果将多项式 (me=k1N)d 展开,那么所有带有N的项模N(%N)都会变成0,只留下第一项med
- 则公式变成 med%N=m
- 所以只要证明 med%N=m 公式成立即可
- 为了使上述公式成立,e d N需要满足以下条件
- 设 r=φ(N)
- 取e: 1<e<r ,且e与r互质
- 由于e与r互质,则可以求出模反元素d: ed%r≡1
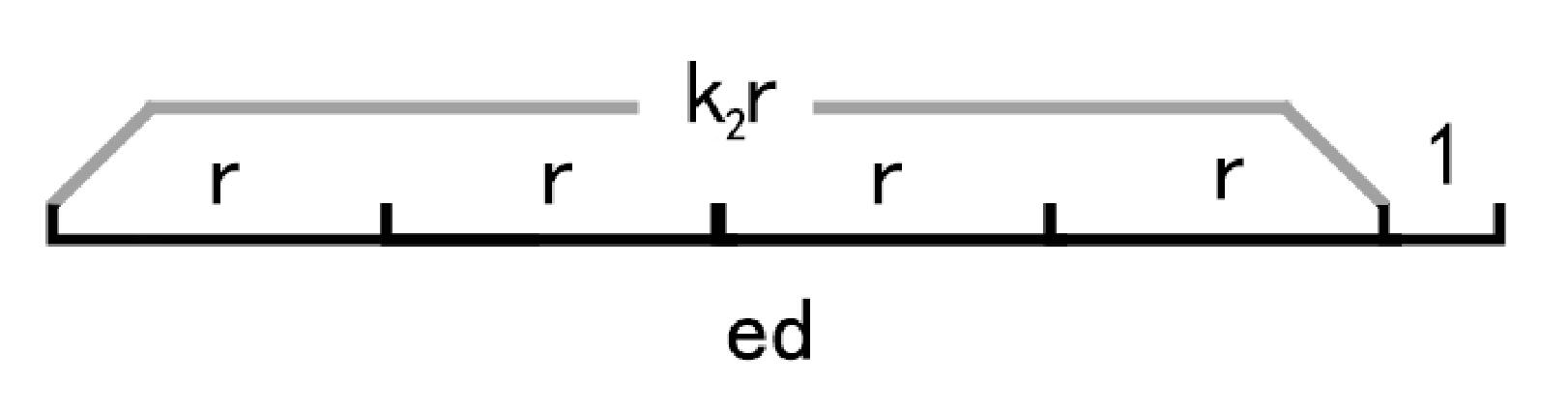
- ed=1+k2r
- 将 ed 代入 med%N=m 中
- 则变成: mk2r+1%N=m
- 接下来将分别展开讨论
- ①如果m与N互质
- 则根据欧拉定理 mφ(N)%N≡1
- mφ(N)=k3N+1
- 因为刚刚设 r=φ(N)
- 公式可写成mr=k3N+1
- 对等式两边同时取k2幂: mk2r=(k3N+1)k2
- 两边再同时乘m: mk2r+1=m(k3N+1)k2
- 再将公式代入mk2r+1%N=m 中
- 得到m(k3N+1)k2%N=m
- 展开左侧多项式后,所有带 N 的项全部消失,只剩下最后一项: m*1k2=m
- m=m,等式成立
- ②如果m与N不互质
- 则取N为两个质数p和q的积
- 即: N=pq (p≠q)
- 这样一来,m一定与p或者q互质
- 假如 m 与 q 互质, 那么 m 一定与 p 成倍数关系: m=k4p
- 如此一来,因为q是质数,根据欧拉定理可以列出公式: mq-1%q=1
- 因为 mq-1 的任意次方,上述等式皆成立
- 所以 mk2(q-1)(p-1)%q=1 同样成立
- 因为刚刚设 r=φ(N)
- 根据欧拉函数性质 r=φ(N)=(q-1)(p-1)
- 则 mk2r%q=1
- 将一开始的公式 ed=1+k2r → k2r=ed-1 代入上式
- 得到 med-1%q=1
- 转换成 med-1=k5q+1
- 两边同时乘以 m 得 med=mk5q+m
- 因为 m=k4p
- 所以上式转换为 med=k4pk5q+m
- 即 med=k4k5(pq)+m
- 因为N=pq
- 所以 med=k4k5N+m
- 即 med%N=m
- 至此,证明完毕
生成秘钥
由此,可以按照上述证明方法生成 公钥 (N, e) | 私钥 (N, d)
- 首先先声明N,N等于两个不相等的质数p和q的积: N=pq
- 然后计算出N的欧拉函数: r=φ(N)=(q-1)(p-1)
- 取e: 1<e<r ,且e与r互质
- 由于e与r互质,可求出模反元素d: ed%r≡1
- 至此可得出公钥 (N, e) | 私钥 (N, d)
代码如下
密钥生成代码: SRAKeyGenerate.java
加密代码: SRAEncrypt.java
解密代码: SRADecrypt.java
可见,这种加密方法与解密方法的所使用的秘钥是不同的
当发送者传递密文的时候,如果被中间人拦截到了,那么只会拦截到解密密钥,而无法篡改信息
要是想要从私钥的d推导出公钥的e的话
那么就需要 ed%r≡1 中的r
而 r 则需要对N的来源 r=φ(N)=(q-1)(p-1) 中 p 和 q 下手
但问题是,p 和 q 是 N=pq 下比 N 小的众多质数中的随意两个
如果这个 N 值取得越大,那么 p 和 q 则越难解
至少以现有的计算机计算速度和分解质数算法中,N达到几百位数的情况下将花费数好久才能解开
当前的技术和方法使得在个人计算机上分解这个问题大约需要一个小时以上:
RSA-100 有 100 个十进制数字(330 位)。 Arjen K. Lenstra 于 1991 年 4 月 1 日宣布了其因式分解
据报道,在 MasPar 并行计算机上使用多项式二次筛算法进行因式分解花费了几天时间。
目前为止,最大的 RSA 数为 768 位(232 个十进制数字),在基于 2.2 GHz AMD Opteron 的单核计算机上需要近 2000 年的计算时间。对 1024 位 RSA 模数进行因式分解大约困难一千倍。
所以N的位数越高,则秘钥越安全
Kryptos
2024年5月5日
正当我写关于这篇博客的草稿阶段时,LEMMiNO更新了一部视频
https://www.youtube.com/watch?v=jVpsLMCIB0Y
视频中讲述了一座位于美国弗吉尼亚州中央情报局(CIA)广场上的雕塑作品,雕塑的一半是由总共865个字符组成的密文,另一半是一个维吉尼亚密码表
该作品于1990年竣工,吸引了无数位破译专家前来解密。
直到现在,密文的第四部分未成功破译
百度百科: 克里普托斯
 Kryptos
Kryptos
作者 Jim Sanborn 并不是一位密码学家,而且他曾声称他其实在数学方面能力很差
对于Jim来说,他更熟悉的是物理,而物理也只是浅尝辄止而已
而在这样的背景下,这个密码却经受住了多年的考验
1999年,南加州的计算机科学家 Jim Gillogly 宣布他成功破译了密文的前三段。而当他公布结果的时候,CIA透露他们的分析师 David Stein 在 1998 年使用铅笔和纸张技术解决了相同的段落
但至此,最后一段仍然是不可破解的谜题
后来,2006年、2010年和2020年,Jim Sanborn分别透露了最后一段密文的几条线索
鉴于 Jim Sanborn 的个人背景来看,或许我们需要跳出密码学的框架来思考问题,也许那样,才能找到最后一段密文的真正“钥匙”
后续,我将对更多诸如摘要算法、语言学、文体学、模因、复合密码、低精度传递信息等等内容展开更多讨论
最近忙的事情太多,完全抽不出时间写博客,第一部分就先这些吧..._(:з」∠)_